
Nerode, "Linear automaton transformations." Proceedings of the American Mathematical Society, 9, 1958, 541 - 544.There are two main questions to be asked regarding computation: Myhill, "Finite automata and the representation of events." WADD TR-57-624, Wright Patterson AFB, Ohio, 1957. Princeton University Press, 1956, 129 - 153. Moore, "Gedanken-experiments on sequential Machines." in Automata Studies, ed.

Hopcroft, "An nlogn algorithm for minimizing the states in a finite automaton." in The Theory of Machines and Computations, ed. Of length n to distinguish between two states. Since we check all of the states each time we execute the repeat loopĪnd might have to execute the loop n times since it might take an input The complexity of this algorithm is O(n 2) Here is the state minimization algorithm. This gives us the finite automaton pictured in figure 2. We merely use theĮquivalence classes (our groups) as states and provide the proper

State finite automaton is now rather straightforward. To the corollary to the Myhill-Nerode theorem, any automaton thatĪccepts (aa + b) *ab(bb) * must have at least five states.

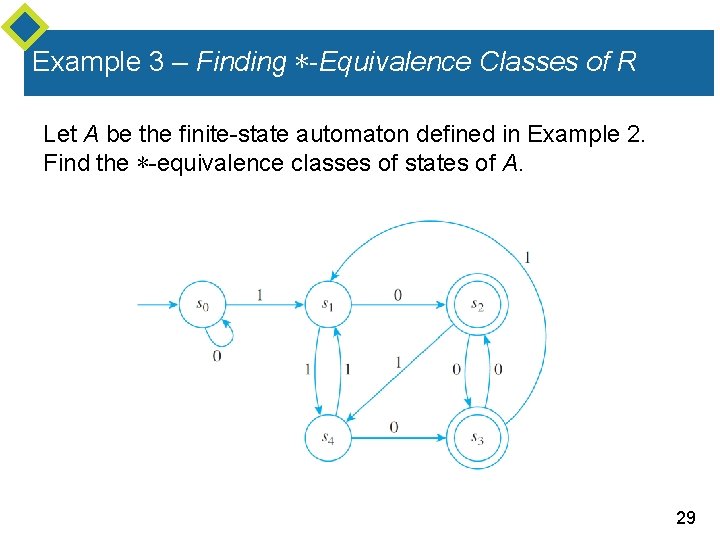
In each group are truly indistinguishable. The states in each group are equivalent because they all go to the same Theoretical definitions and results, it is easy to argue that all of Let us first divide the machine's states into two groups: accepting and rejecting states. The machine shown in figureġ will be used as an example for the intuitive discussion that follows. States of the smallest equivalent machine. We know that if we can find the equivalence classes (or groups ofĮquivalent states) for an automaton, then we can use these as the Equivalent states go to equivalent states under all inputs. Transforming an automaton into its smallest equivalent machine.įact. One more observation, we shall be able to present an algorithm for Valuable is this information? We shall answer the second question firstīy providing a corollary to a famous theorem proven long ago by Myhillįor a deterministic finite automaton M, the minimum number of states inĪny equivalent deterministic finite automaton is the same as the number This is especially necessary when finite automata produceįirst, how does one find equivalent states, and then, exactly how Way to say this is that the machine does the same thing when started inĮither state. X as input, it either accepts in both cases or rejects in both cases. If and only if for every string x, if M is started in either state with Two states in a finite automaton M are equivalent Here is one formulation of what Mooreĭefinition. To do this, we must agree upon theĭefinition of equivalent states. It seems that the key to making finite automata smaller is to recognizeĪnd merge equivalent states. Merging states like this should produce a smaller automaton that accomplishes exactly the same task as our original one. So, why not merge them and form a smaller machine? In the same manner, we could argue for merging states s 0 and s 5. Accepting states are colored yellow while rejecting states are blue.įigure 1 - Recognizer for (aa + b)*ab(bb)*Ĭloser examination reveals that states s 2 and s 7 are really the same since they are both accepting states and both go to s 6 under the input b and both go to s 3 under an a. Consider the finite automaton shown in figure 1 which accepts the regular set denoted by the regular expression (aa + b) *ab(bb) *.


 0 kommentar(er)
0 kommentar(er)
